Exercícios resolvidos de porcentagem

1) Quanto é 15% de 80?

Multiplique 15 por 80 e divida por 100:

Se você achar mais fácil, você pode simplesmente multiplicar 15% na sua forma decimal, que é 0,15 por 80:

15% de 80 é igual a 12.

2) Quanto é 70% de 30?

Multiplique 70 por 30 e divida por 100:

Ou então você pode multiplicar 70% na sua forma decimal, que é 0,70 por 30:

70% de 30 é igual a 21.

3) Quanto é 150% de 45?

Multiplique 150 por 45 e divida por 100:

Você também pode simplesmente multiplicar 150% na sua forma decimal, que é 1,50 por 45:

150% de 45 é igual a 67,5.

4) Quanto é 100% de 40?

Multiplique 100 por 40 e divida por 100:

Se você preferir pode multiplicar 100% na sua forma decimal, que é 1,00 por 40:

Na verdade você não precisa fazer conta alguma. Como você já sabe 100% representa o todo, por isto 100% de qualquer número será sempre o próprio número.

100% de 40 é igual a 40.

5) Expresse a razão de 19 para 25 como uma porcentagem.

A razão de 19 para 25 pode ser expressa nestas duas formas:

Ao realizarmos a divisão de 19 por 25 iremos obter o valor da razão:

Tal como procedemos no caso das razões centesimais, devemos multiplicar este valor decimal por cem e acrescentar o símbolo "%" para termos a representação da porcentagem, na verdade o multiplicamos por 100%:

Assim 19 : 25 na forma de porcentagem é igual a 76%.

6) 30% da população de uma cidade litorânea mora na área insular e os demais 337.799 habitantes moram na área continental. Quantas pessoas moram na ilha?

Sabemos que 30% da população da cidade mora na ilha e o restante 100 % - 30%, ou seja, 70% mora no continente. Como 70% corresponde a 337.799habitantes, podemos montar uma regra de três para calcularmos quantos habitantes correspondem aos 30% que moram na ilha:

337.799 está para 70, assim como x está para 30:

Podemos resolver este exercício de uma outra forma. Se multiplicarmos337.799 por 100 e dividirmos este produto por 70, iremos encontrar o número total de habitantes da cidade:

Ao calcular 30% de 482.570 iremos encontrar o número de habitantes da ilha:

Portanto a população da cidade que mora na área insular é de 144.771 habitantes.

7) Se 4% de um número é igual a 15, quanto é 20% deste número?

Se dividirmos 15 por 0,04, que é equivalente a 4% na sua forma decimal, iremos obter o número que 4% dele é igual a 15:

Para calcularmos 20% de 375 basta multiplicá-lo por 0,20:

Em uma única conta faríamos:

Note que concluímos multiplicando 15 por 5, o que fica bastante claro se pensarmos que 20% também é cinco vezes 4%.

20% do referido número é igual a 75.

8) Do meu salário R$ 1.200,00 tive um desconto total de R$ 240,00. Este desconto equivale a quantos por cento do meu salário?

Vamos resolver este exercício montando uma regra de três:

O percentual que eu procuro (x) está para o desconto (R$ 240,00), assim como 100% está para o meu salário deR$ 1.200,00:

Portanto este desconto equivale a 20% por cento do meu salário.

9) Eu tenho 20 anos. Meu irmão tem 12 anos. A idade dele é quantos por cento da minha?

Sem utilizarmos uma regra de três, basta que se divida o valor do qual se procura a porcentagem (12), pelo valor que representa os 100% (20) e que se multiplique o valor obtido por 100%:

Portanto a idade de meu irmão é 60% da minha idade.

10) Meu carro alcança uma velocidade máxima de 160 km/h. O carro de meu pai atinge até 200 km/h. A velocidade máxima do carro do meu pai é quantos por cento da velocidade máxima do meu carro?

Basta que se dividamos o valor do qual se procura a porcentagem (200), pelo valor que representa os 100% (160) e que se multiplique o valor obtido por 100%:

Portanto a velocidade máxima do carro do meu pai é 125% da velocidade máxima do meu carro. O percentual encontrado (125%) é maior que 100% porque o carro de meu pai é 25% mais veloz que o meu.

11) Por um descuido meu, perdi R$ 336,00 dos R$ 1.200,00 que eu tinha em meu bolso. Quantos por cento eu perdi desta quantia?

R$ 336,00 é 28% de R$ 1.200,00. Obtemos este valor dividindo-se 336 por 1200:

0,28 está na forma decimal, então o multiplicamos por 100% para colocá-lo na sua forma percentual: 28%.

Portanto:

 Eu perdi 28% desta quantia.

12) Dei ao meu irmão 25 das 40 bolinhas de gude que eu possuía. Quantos por cento das minhas bolinhas de gude eu dei a ele? Com quantos por cento eu fiquei?

25 é 62,5% de 40. Obtemos este valor pela divisão de 25 por 40:

0,625 está na sua forma decimal, então o multiplicamos por 100% para colocá-lo na sua forma percentual: 62,5%. Este é o percentual de bolinhas que eu dei.

A diferença entre 40 e 25 é 15. Como 40 equivale a 100% e 25 equivale a 62,5%, então 15 equivale à diferença entre 100% e 62,5% que é 37,5%:

Chegaríamos também aos mesmos 37,5% se tivéssemos divido 15 que é a quantidade de bolinhas que ficaram comigo, por 40 que é a quantidade total.

Portanto:

 Eu dei 62,5% das bolinhas de gude que eu possuía e fiquei com 37,5%.

13) Ao comprar um produto que custava R$ 1.500,00 obtive um desconto de 12%. Por quanto acabei pagando o produto? Qual o valor do desconto obtido?

12% de R$ 1.500,00 é R$ 180,00. Chegamos a este valor pela conta abaixo:

A diferença entre R$ 1.500,00 e R$ 180,00 é de R$ 1.320,00, conforme calculado a seguir:

Portanto:

 Com o desconto percentual obtido de 12%, em valor obtive R$ 180,00 de desconto e acabei pagando R$ 1.320,00.

14) Na festa de aniversário do meu sobrinho derrubei uma mesa onde estavam 40 garrafas de refrigerante. Sobraram apenas 15% das garrafas sem quebrar. Quantas garrafas sobraram e quantas eu quebrei?

15% de 40 é 6. Chegamos a este valor pela conta abaixo:

A diferença entre 40 e 6 é de 34, conforme calculado a seguir:

Portanto:

 Das 40 garrafas que estavam na mesa, eu quebrei 34 e sobraram apenas 6.

15) Dos 28 bombons que estavam na minha gaveta, já comi 75%. Quantos bombons ainda me restam?

75% de 28 é 21. Chegamos a este valor pela conta abaixo:

A diferença entre 28 e 21 é de 7, conforme calculado a seguir:

7 é o número de bombons que ainda me restam, mas poderìamos ter chegado a este resultado por outro caminho.

Como eu já comi 75% dos 100% dos bombons que eu possuía, ainda tenho 25% deles, basta então calcularmos quanto é 25% de 28:

Portanto:

 Dos 28 bombons ainda me restam 7.

16) Em uma cesta eu possuía uma certa quantidade de ovos. As galinhas no meu quintal botaram 10% da quantidade dos ovos que eu tinha na cesta e nela os coloquei, mas por um azar meu, um objeto caiu sobre a dita cuja e 10% dos ovos foram quebrados. Eu tenho mais ovos agora ou inicialmente?

Digamos que originalmente eu tivesse x ovos. Como você sabe 10% pode ser escrito como 0,1 já que 10% equivale a 10 divididos por 100. Desde que minhas galinhas botaram uma quantidade equivalente a 10% da que eu possuía, isto equivale a dizer que além dos x ovos originais, agora eu possuo mais 0,1x, ou seja, agora eu tenho 1,1x ovos:

Só que quando eu tinha 1,1x ovos eu acabei perdendo 10% deles, ou seja, fiquei com 90% dos ovos, já que dos 100% eu perdi 10%:

0,99x representa 99% dos ovos que eu tinha originalmente e já que eu tinha 100%, ao ficar com 99% fiquei com 1% a menos que a quantidade original.

Portanto:

 Inicialmente eu tinha mais ovos que agora.

De forma resumida, a quantidade original de ovos pode ser representada pelo número 1 (100% dos ovos).

Como foram acrescentados mais 10%, este acréscimo de 10% equivale a 100% + 10%, ou seja, equivale a 110% que é equivalente a 1,1.

Ao perder 10% eu fiquei apenas com 90% dos ovos, ou seja, fiquei com 0,9 deles.

Multiplicando-se tais valores teremos:

Estes 99% são os ovos que ainda me restam.

17) O aumento salarial de uma certa categoria de trabalhadores seria de apenas 6%, mas devido à intervenção do seu sindicato, esta mesma categoria conseguiu mais 120% de aumento sobre o percentual original de 6%. Qual foi o percentual de reajuste conseguido?

Estamos falando de acréscimo de porcentagem de porcentagem, já que os 6% originais foram aumentados em 120%. Vejamos como vai ficar a resolução:

Ou seja, o aumento conseguido foi de 13,2%, mas podemos pensar na resolução do problema de uma outra forma:

O aumento conseguido originalmente era de 6%, este percentual equivale a 100% do aumento conseguido, mas como conseguiu-se mais 120% de aumento, então o passamos a ter 220% ( 100% + 120%) de aumento sobre os 6%, logo o problema consiste em se calcular 220% de 6%:

Portanto:

 O percentual de reajuste conseguido pela categoria foi 13,2%.

18) Quanto é 60% de 200% de 80%?

Neste tipo de exercício devemos multiplicar todos os percentuais. Todos eles devem ser passados para a sua forma decimal, exceto o último:

Portanto:

60% de 200% de 80% é igual a 96%

19)  Comprei um frango congelado que pesava 2,4kg. Após o descongelamento e de ter escorrido toda a água, o frango passou a pesar apenas 1,44kg. Fui lesado em quantos por cento do peso, por ter levado gelo a preço de frango?

Se dividirmos 0,96, que corresponde ao peso do gelo, por 2,4, que corresponde ao peso total, iremos obter 0,4, que se multiplicado por 100, nos dará o percentual procurado:

Fui lesado em 40% do peso. É este o percentual equivalente aos 960g de gelo que paguei como se fosse frango.

20) Tempos atrás o rolo de papel higiênico que possuiu por décadas 40 metros de papel, passou a possuir apenas 30 metros. Como o preço do rolo não sofreu alteração, tal artimanha provocou de fato um aumento de quantos por cento no preço do metro do papel?

Vamos dizer que originalmente o rolo custasse x, então o preço do metro de papel seria .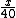

Depois o rolo ainda custava x, mas o preço do metro de papel seria 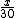, que seria obviamente maior que antes, já que temos menos papel ao mesmo custo.

Ao dividirmos 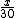 por 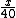 e subtrairmos 1 iremos obter na forma decimal qual foi o aumento no preço do produto:

Como sabemos, aproximadamente 0,3333 na forma decimal equivale a 33,33%.

Como você pode ter reparado a variável x utilizada na solução do problema acabou sendo simplificada por ela mesma. De forma mais simples em exercícios deste tipo você pode simplesmente realizar as contas tal como abaixo:

Tal artimanha provocou o aumento de cerca de 33,33% no preço do metro do papel.