Matemática para Contadores: agosto 2013

Noções de Razão

Vamos considerar um carro de corrida com 4m de comprimento e um kart com 2m de comprimento. Para compararmos as medidas dos carros, basta dividir o comprimento de um deles pelo outro. Assim:

(o tamanho do carro de corrida é duas vezes o tamanho do kart).

Podemos afirmar também que o kart tem a metade

do comprimento do carro de corrida.

A comparação entre dois números racionais, através de uma divisão, chama-se razão.

A razão

pode também ser representada por 1:2 e significa que cada metro do kart corresponde a 2m do carro de corrida.

Denominamos de razão entre dois números a e b (b diferente de zero)
o quociente

ou a:b.

A palavra razão, vem do latim ratio, e significa "divisão". Como no exemplo anterior, são diversas as situações em que utilizamos o conceito de razão.

Exemplos:

Dos 1200 inscritos num concurso, passaram 240 candidatos.
Razão dos candidatos aprovados nesse concurso:

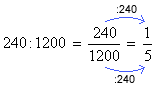(de cada 5 candidatos inscritos, 1 foi aprovado).

Para cada 100 convidados, 75 eram mulheres.
Razão entre o número de mulheres e o número de convidados:

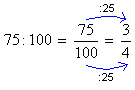(de cada 4 convidados, 3 eram mulheres).

Observações:

1) A razão entre dois números racionais pode ser apresentada de três formas. Exemplo:
Razão entre 1 e 4: 1:4 ou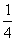

ou 0,25.

2) A razão entre dois números racionais pode ser expressa com sinal negativo, desde que seus termos tenham sinais contrários. Exemplos:

A razão entre 1 e -8 é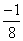

A razão entre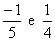

Exercícios resolvidos de razão

Exercícios de Razões

a) A razão é igual a 10. Determine a razão .

b) A distância entre duas cidades num mapa de escala 1:2000 é de 8,5 cm. Qual a distância real entre essas duas cidades?

c) A idade de Pedro é 30 anos e a idade de Josefa é 45 anos. Qual é a razão entre as idades de Pedro e Josefa?

d) Uma caixa de chocolate possui 250g de peso líquido e 300g de peso bruto. Qual é a razão do peso líquido para o peso bruto?

e) A razão entre o comprimento da sombra e da altura de um edifício é de . Se o edifício tem 12 m de altura, qual o comprimento da sombra?

Resposta dos Exercícios

A palavra proporção vem do latim proportione e significa uma relação entre as partes de uma grandeza, ou seja, é uma igualdade entre duas razões.

No século XV, o matemático árabe Al-Kassadi empregou o símbolo "..." para indicar as proporções e em 1537, o italiano Niccola Fontana, conhecido por Tartaglia, escreveu uma proporção na forma 6:3::8:4. Regiomontanus foi um dos matemáticos italianos que mais divulgou o emprego das proporções durante o período do Renascimento.

Denomina-se proporção a igualdade entre duas razões. Considerando a, b, c e d, diferentes de zero, podemos afirmar que eles constituem respectivamente uma proporção se:

Nesse caso, a, b, c e d são chamados de termos da proporção.

Exemplo:

Consideremos os números 6, 8, 9, 12, vemos que a razão do primeiro para o segundo (6 : 8) e a razão do terceiro para o quarto (9 : 12) são iguais. Logo, pode-se escrever:

Diz-se nesse caso, que os números 6, 8, 9, 12, nessa ordem, formam uma proporção. Daí percebe-se que proporção é a igualdade de duas razões.

Os números 6, 8, 9, 12 são chamados termos da proporção, onde o primeiro e o quarto termos chamam-se extremos; o segundo e o terceiro meios.

Propriedade fundamental das proporções
Nas razões iguais, o produto dos extremos deve ser igual ao produto dos meios ou vice-versa. Ou seja,

Resolução de uma proporção quando um dos termos é desconhecido

Resolver uma proporção é determinar o valor de X (termo desconhecido) para o qual a igualdade é verdadeira.

Algumas observações:

1. Em toda proporção, a soma dos dois primeiros termos está para o primeiro (ou para o segundo) termo, assim como a soma dos dois últimos termos está para o terceiro (ou para o quarto) termo. Assim,

2. Em toda proporção, a soma do antecedente está para a soma dos conseqüentes, assim como cada antecedente está para seu conseqüente. Assim,

Propriedades das Proporções

Para a proporção

A B	=	C D

valem as seguintes propriedades:

O produto dos meios é igual ao produto dos extremos, isto é:

A · D = B · C
A soma (diferença) dos dois primeiros termos está para o primeiro termo, assim como a soma (diferença) dos dois últimos está para o terceiro termo, isto é:

A+B

A = C+D

C e A-B

A = C-D

C
A soma (diferença) dos dois primeiros termos está para o segundo termo, assim como a soma (diferença) dos dois últimos está para o quarto termo, isto é:

A+B

B = C+D

D e A-B

B = C-D

D
A soma (diferença) dos antecedentes está para a soma (diferença) dos consequentes, assim como cada antecedente está para o seu consequente, isto é:

A+C

B+D = A

B = A-C

B-D e A+C

B+D = A-C

B-D = C

D

Video Aula sobre razões e proporções

Esta vídeo aula vai te ajudar a entender os conceitos de razão e proporção. Este assunto está sempre presente no ENEM e as ilustrações vão deixar tudo mais fácil.

Vejam os vídeos:

Voltar a página principal

Exercícios resolvidos de proporções

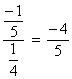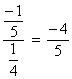1) Dois números somados totalizam 510. Sabe-se que um deles está para 8, assim como o outro está para 9. Quais são os dois números?

Chamemos o primeiro número de a e o outro número de b. Do enunciado, tiramos que a está para 8, assim como bestá para 9. Utilizando-nos da terceira propriedade das proporções temos:

Sabemos que a e b somados resultam em 510, assim como a adição de 8 a 9 resulta em 17. Substituindo estes valores na proporção teremos:

Portanto:

Chegamos então que os dois números são 240 e 270.

2) Um número a somado a um outro número b totaliza 216. a está para 12, assim como b está para 15. Qual o valor de a e de b?

Recorrendo à terceira propriedade das proporções montamos a seguinte proporção:

Sabemos que a soma de a com b é igual a 216, assim como também sabemos que 12 mais 15 totaliza 27. Substituindo tais valores teremos:

Portanto:

Os dois números são 96 e 120.

3) Um número a subtraído de um outro número b resulta em 54. a está para 13, assim como b está para 7. Qual o valor de a e de b?

Recorremos à terceira propriedade das proporções para montarmos a seguinte proporção:

Sabemos que a diferença entre a e b é igual a 54, e sabemos também que 13 menos 7 dá 6. Substituindo tais valores teremos:

Portanto:

Os dois números são 117 e 63.

4) A diferença entre dois números é igual a 52. O maior deles está para 23, assim como o menor está para 19. Quais são os números?

Vamos chamar o número maior de a e o menor de b. Do enunciado, a está para 23, assim como b está para 19. Ao utilizarmos a terceira propriedade das proporções temos:

Sabemos que a menos b é igual a 52, assim como 23 menos 19 é igual a 4. Ao substituirmos estes valores na proporção teremos:

Portanto:

Chegamos então que os dois números são 299 e 247.

5) A idade de Pedro está para a idade de Paulo, assim como 5 está para 6. Quantos anos tem Pedro e Paulo sabendo-se que as duas idades somadas totalizam 55 anos?

Identifiquemos a idade de Pedro por a e a idade de Paulo por b. A partir do enunciado, temos que a está para b, assim como 5 está para 6. Utilizando-nos da segunda propriedade das proporções temos:

Sabemos que a soma a e b resulta em 55, assim como 5 mais 6 resulta em 11. Substituindo estes valores na proporção temos:

Para calcularmos o valor de a temos:

Portanto:

Pedro tem 25 anos e Paulo tem 30 anos.

6) O peso de uma sacola em kg está para o peso de uma outra sacola também em kg, assim como 32 está para 28. Quanto pesa cada uma das sacolas, sabendo-se que juntas elas pesam 15kg?

Identifiquemos o peso da primeira sacola por a e o peso da segunda por b. Como expresso no enunciado, temos que a está para b, assim como 32 está para 28. Da segunda propriedade das proporções temos que:

Temos que a e b somados resultam em 15, assim como 32 mais 28 resulta em 60. Substituindo-os na proporção temos:

Calculemos o valor de b:

Portanto:

Uma das sacolas pesa 8kg ao passo que a outra pesa 7kg.

7) A soma de dois números é igual a 46. O primeiro está para o segundo, assim como 87 está para 51. Quais são os números?

Identifiquemos o primeiro deles por a e o segundo por b. Como dito no enunciado, a está para b, assim como 87está para 51. A segunda propriedade das proporções nos diz que: